[프로그래머스] 퍼즐 조각 채우기 / 깊이,너비 우선 탐색(DFS/BFS) / python

문제

https://school.programmers.co.kr/learn/courses/30/lessons/84021

프로그래머스

 

 

테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈 공간에 적절히 올려놓으려 합니다. 게임 보드와 테이블은 모두 각 칸이 1x1 크기인 정사각 격자 모양입니다. 이때, 다음 규칙에 따라 테이블 위에 놓인 퍼즐 조각을 게임 보드의 빈칸에 채우면 됩니다.

• 조각은 한 번에 하나씩 채워 넣습니다.
• 조각을 회전시킬 수 있습니다.
• 조각을 뒤집을 수는 없습니다.
• 게임 보드에 새로 채워 넣은 퍼즐 조각과 인접한 칸이 비어있으면 안 됩니다.

다음은 퍼즐 조각을 채우는 예시입니다.

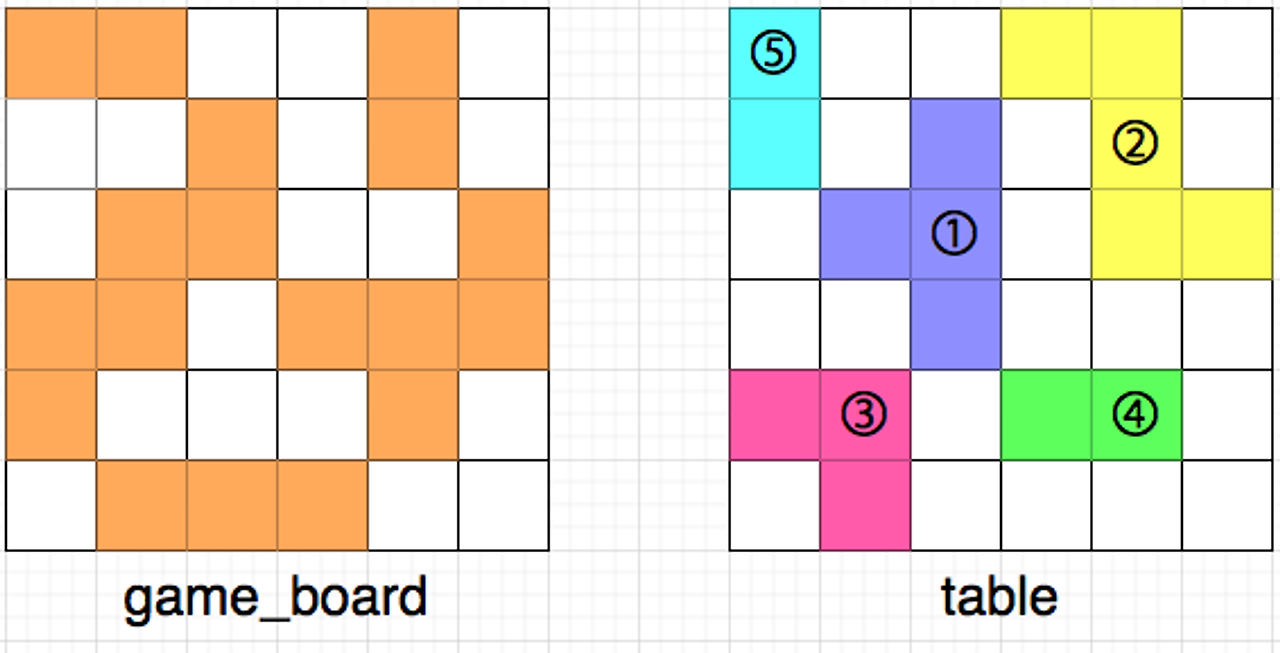
위 그림에서 왼쪽은 현재 게임 보드의 상태를, 오른쪽은 테이블 위에 놓인 퍼즐 조각들을 나타냅니다. 테이블 위에 놓인 퍼즐 조각들 또한 마찬가지로 [상,하,좌,우]로 인접해 붙어있는 경우는 없으며, 흰 칸은 퍼즐이 놓이지 않은 빈 공간을 나타냅니다. 모든 퍼즐 조각은 격자 칸에 딱 맞게 놓여있으며, 격자 칸을 벗어나거나, 걸쳐 있는 등 잘못 놓인 경우는 없습니다.

이때, 아래 그림과 같이 3,4,5번 조각을 격자 칸에 놓으면 규칙에 어긋나므로 불가능한 경우입니다.

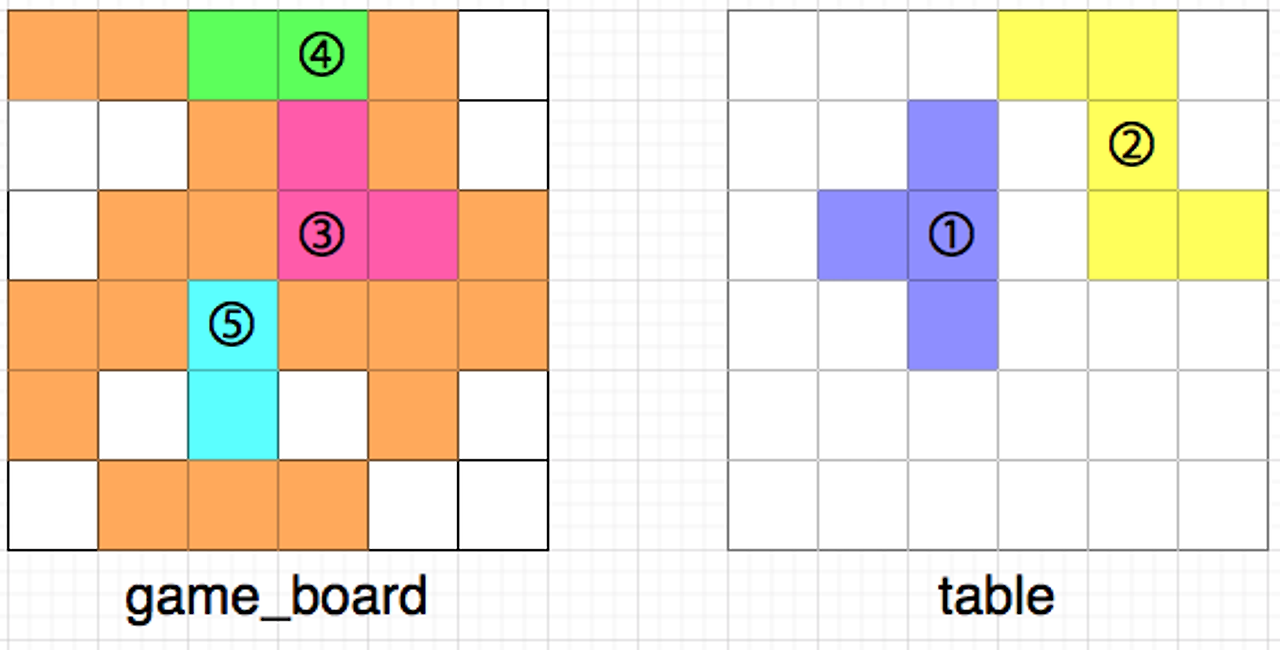
• 3번 조각을 놓고 4번 조각을 놓기 전에 위쪽으로 인접한 칸에 빈칸이 생깁니다.
• 5번 조각의 양 옆으로 인접한 칸에 빈칸이 생깁니다.

다음은 규칙에 맞게 최대한 많은 조각을 게임 보드에 채워 넣은 모습입니다.

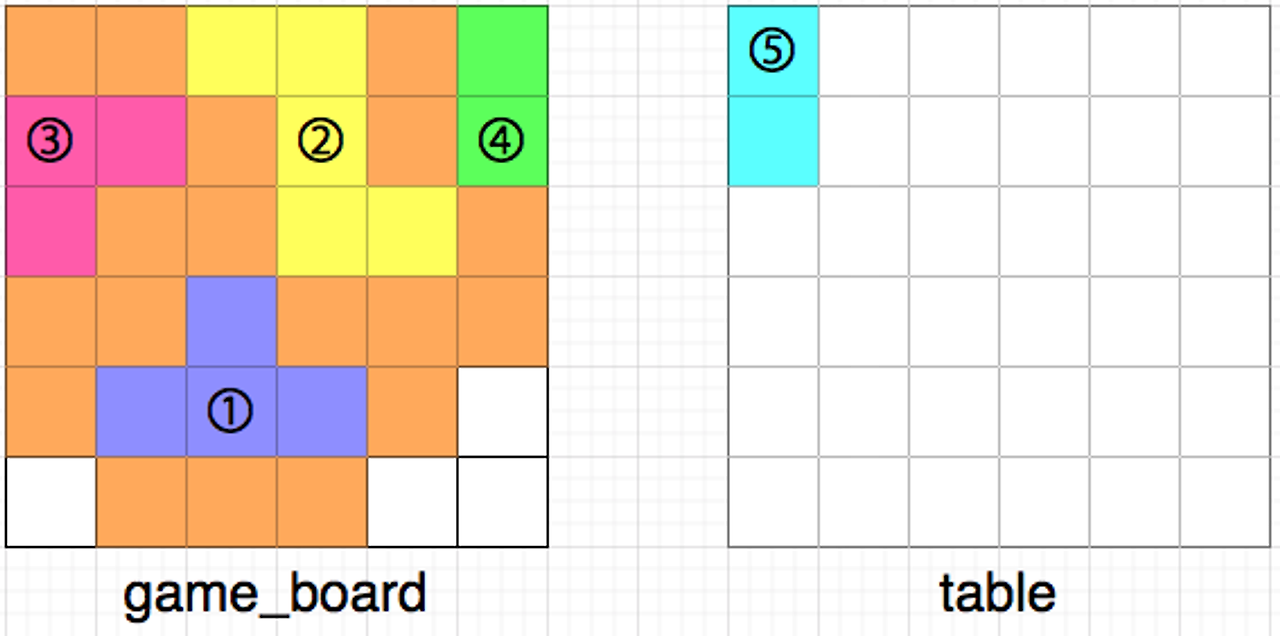
최대한 많은 조각을 채워 넣으면 총 14칸을 채울 수 있습니다.

현재 게임 보드의 상태 game_board, 테이블 위에 놓인 퍼즐 조각의 상태 table이 매개변수로 주어집니다. 규칙에 맞게 최대한 많은 퍼즐 조각을 채워 넣을 경우, 총 몇 칸을 채울 수 있는지 return 하도록 solution 함수를 완성해주세요.

 

제한사항

• 3 ≤ game_board의 행 길이 ≤ 50
• game_board의 각 열 길이 = game_board의 행 길이
• table의 행 길이 = game_board의 행 길이
• table의 각 열 길이 = table의 행 길이
• game_board에는 반드시 하나 이상의 빈칸이 있습니다.
• table에는 반드시 하나 이상의 블록이 놓여 있습니다.

 

풀이

아이디어

블럭을 이용해서 문제를 푼다는 것에서 이전에 풀었던 상어중학교랑 비슷하다는 생각이 들었다

물론 상어중학교가 더 어려웠음..

 

사실 BFS보단 구현에 더 가까운 느낌

전체 빡 구현 안에 자그마한 BFS가 이용된다고 보면 될 듯

구현 문제는 일단 전체적으로 해야할 일을 정해놓고 하나씩 퀘스트 깨듯 풀어내면 놓치지 않고 구현할 수 있다

(근데도 하나 놓친 부분때문에 소노)

 

구현문제는 해야할 일들을 하나씩 함수를 이용하면 더 깔끔하게 표현가능하다

디버깅이 쉬워지는 것까지 포함

우리 교수님은 함수 활용을 잘해야한다고 항상 강조..하셨더랬지..

 

👏🏻 할 일

1. 게임 보드에서 빈칸 조각을 찾음
2. 테이블에서 조각을 찾음
3. 조각 비교를 위해 절대적인 위치 설정
4. 회전

 

 

조각 찾기 search_puzzle

BFS가 사용되는 구간

조각 찾기는 2번 실행하기 때문에 함수로 활용하는 것이 좋다

 

game_board에서는 빈칸을, table에서는 채워진 칸을 찾아야 하기 때문에 주의를 요함!

두개가 반대로 움직이는 것을 이용했다

배열의 인덱스와 원소를 이용함 state[0,1]

 

from collections import deque

state_list = [1, 0]

def search_puzzle(board, blocks, state):
    visited = [[0] * N for _ in range(N)]
    for i in range(N):
        for j in range(N):
            # game: 1, table 0(빈칸)일때 스킵
            if board[i][j] == state_list[state] or visited[i][j]: continue
            blocks.append(bfs(i,  j, board,visited, state))
    blocks.sort(key = lambda x: len(x), reverse = True)

# 격자 내부인지 아닌지 확인
def is_board(x, y):
    return 0 <= x < N and 0 <= y < N

# 퍼즐 조각 찾기, state(board 0/ table 1)
def bfs(x, y, board,visited, state):
    # 좌, 우, 위, 아래
    dx = [-1, 1, 0, 0]
    dy = [0, 0, 1, -1]
    
    q = deque()
    q.append([x, y])
    puzzle = [[x, y]]

    while q:
        x, y = q.popleft()
        visited[x][y] = 1

        for d in range(4):
            nx = x + dx[d]
            ny = y + dy[d]
            # 격자 내부 존재하지 않거나 방문한 경우
            if not is_board(nx, ny):
                continue
            if visited[nx][ny] == 1:
                continue
            # 빈 칸인 경우
            if board[nx][ny] == state:
                visited[nx][ny] = 1
                q.append([nx, ny])
                puzzle.append([nx,ny])
    return puzzle

 

조각 비교를 위한 위치설정

고민이 조금 필요했던 구간

처음엔 전체를 이동시켜서 0,0을 기준으로 보면 어떨까 생각이 들었다

계속 좌표를 이용하면 더 생각하기 복잡할 것 같은 느낌..

 

조각을 감싸는 형태의 이차원배열을 만들어 단순 비교하는 것으로 결정

 

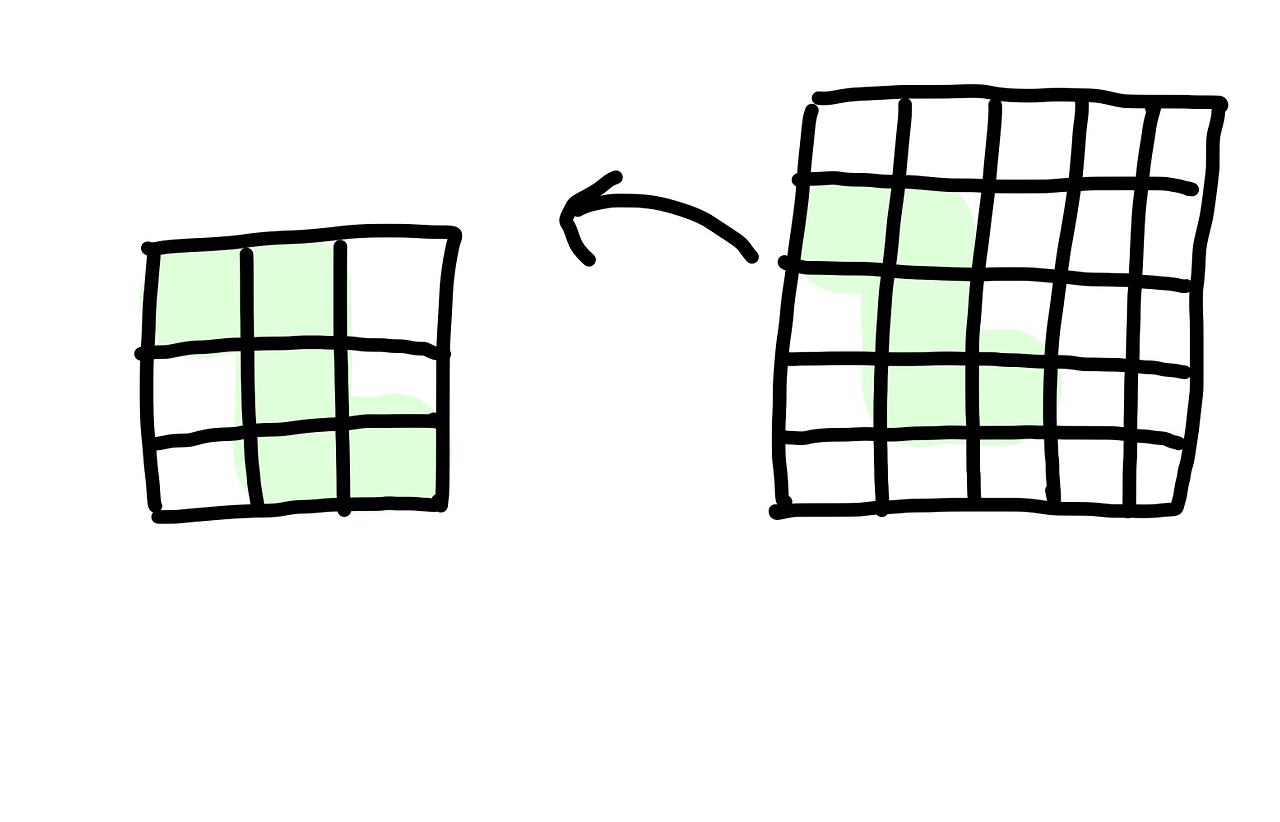
이차원배열 temp의 크기는 가장자리에 있는 좌표의 차로 구할 수 있다

x끼리 y끼리 min과 max를 빼서 간단하게 구함

만들어진 temp 에 0과 1을 이용해 조각을 표시한다

 

# 각 조각을 넣는 이차원 배열
def cover_puzzle(puzzle):
    x = [i[0] for i in puzzle]
    y = [i[1] for i in puzzle]

    r = max(y) - min(y) + 1
    c = max(x) - min(x) + 1
    temp = [[0] * r for _ in range(c)]

    for i, j in puzzle:
        temp[i-min(x)][j-min(y)] = 1
    return temp

회전

상어 친구들 할때 정말 많이 나왔던.. 회전..

그땐 계속 NxN으로 하느라 NxM이 나오니 살짝 헷갈림

회전하는 방향 상관없이 4번다 확인해야하니 생각하기 쉬운 시계방향으로 회전

 

temp[j][r-1-i] = puzzle[i][j]

 

 

# 조각을 회전(시계 90)
def rotate(puzzle):
    cnt = 0
    r, c = len(puzzle), len(puzzle[0])
    temp = [[0] * r for _ in range(c)]
    for i in range(r):
        for j in range(c):
            if puzzle[i][j] == 1: cnt += 1
            temp[j][r-1-i] = puzzle[i][j]
    return temp, cnt

코드

from collections import deque
def search_puzzle(board, blocks, state):
    visited = [[0] * N for _ in range(N)]
    for i in range(N):
        for j in range(N):
            # game: 1, table 0(빈칸)일때 스킵
            if board[i][j] == state_list[state] or visited[i][j]: continue
            blocks.append(bfs(i,  j, board,visited, state))
    blocks.sort(key = lambda x: len(x), reverse = True)

state_list = [1, 0]
def solution(game_board, table):
    global N

    N = len(game_board)
    game_blocks, table_blocks = [], []

    # 1. 조각 찾기
    search_puzzle(game_board, game_blocks, 0)
    search_puzzle(table, table_blocks, 1)


    answer = 0

    for empty in game_blocks:
        flag = False
        # 2. 절대 위치 변경
        game_puzzle = cover_puzzle(empty)

        for table_block in table_blocks:
            # 이미 빈칸을 채웠음을 나타냄
            if flag == True:    break
            # 조각의 개수가 적은 경우 볼 필요가 없음
            if len(game_puzzle) > len(table_block):
                continue
            table_puzzle = cover_puzzle(table_block)
            
            for _ in range(4):
                # 3. 회전
                table_puzzle, cnt = rotate(table_puzzle)

                if table_puzzle == game_puzzle:
                    answer += cnt
                    table_blocks.remove(table_block)
                    flag = True
                    break
    return answer


# 각 조각을 넣는 이차원 배열
def cover_puzzle(puzzle):
    x = [i[0] for i in puzzle]
    y = [i[1] for i in puzzle]

    r = max(y) - min(y) + 1
    c = max(x) - min(x) + 1
    temp = [[0] * r for _ in range(c)]

    for i, j in puzzle:
        temp[i-min(x)][j-min(y)] = 1
    return temp

# 조각을 회전(시계 90)
def rotate(puzzle):
    cnt = 0
    r, c = len(puzzle), len(puzzle[0])
    temp = [[0] * r for _ in range(c)]
    for i in range(r):
        for j in range(c):
            if puzzle[i][j] == 1: cnt += 1
            temp[j][r-1-i] = puzzle[i][j]
    return temp, cnt

# 격자 내부인지 아닌지 확인
def is_board(x, y):
    return 0 <= x < N and 0 <= y < N

# 퍼즐 조각 찾기, state(board 0/ table 1)
def bfs(x, y, board,visited, state):
    # 좌, 우, 위, 아래
    dx = [-1, 1, 0, 0]
    dy = [0, 0, 1, -1]
    
    q = deque()
    q.append([x, y])
    puzzle = [[x, y]]

    while q:
        x, y = q.popleft()
        visited[x][y] = 1

        for d in range(4):
            nx = x + dx[d]
            ny = y + dy[d]
            # 격자 내부 존재하지 않거나 방문한 경우
            if not is_board(nx, ny):
                continue
            if visited[nx][ny] == 1:
                continue
            # 빈 칸인 경우
            if board[nx][ny] == state:
                visited[nx][ny] = 1
                q.append([nx, ny])
                puzzle.append([nx,ny])

    return puzzle